Alternating-sum statistics for certain sets of integers

Jonah Saks and I have uploaded our paper “Alternating-sum statistics for certain sets of integers” to the arXiv. We show that if ${\cal F}$ is a set family in our class, then a certain alternating-sum statistic is constant. This constant equals $-1$ in the case where ${\cal F}$ is the set of all finite primitive sets. Towards the end of the paper, we generalise the notion of primitive sets to $s$-multiple sets and show that if $s\ge 2$, then the alternating-sum statistic we study is not constant, but as $n$ increases it equals $(-1)^s {n-2\choose s-1}$.

Arithmetic constraints on finite sets

As a starting point, consider the following definitions. A set $S$ of integers is said to be

1. primitive if for any two distinct $i,j\in S$, $i$ does not divide $j$;
2. pairwise coprime if any two distinct $i,j\in S$ have $\gcd(i,j) = 1$; and
3. product-free if for any $i,j\in S$ not necessarily distinct, $ij\notin S$.

We consider only finite sets in this post, and as a first observation, we note that taking $S$ to be any subset of the primes, we satisfy all three conditions. Let’s talk about primitive sets first. We will count the number of primitive subsets of \([n] = \{1,2,\ldots,n\}\) that have size exactly $k$, for $0\le k\le n$. Letting $P_{n,k}$ be the number of such sets, here is a table for small $n$:

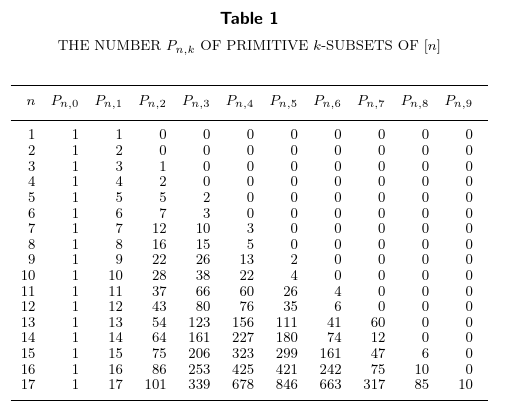
For example, \(P_{6,3} = 3\) because there are three primitive subsets of \(\{1,\ldots,6\}\) that have size exactly $3$, namely, \(\{2,3,5\}\), \(\{3,4,5\}\), and \(\{4,5,6\}\). Taking the alternating sum of this whole row corresponding to $n=6$, we have a value of $1-6+7-3 = -1$, and if you stare at the table, you’ll notice that the alternating sum of each row (except the first one) equals $-1$. Now look at the table for $Q_{n,k}$, the number of pairwise coprime subsets of $[n]$ of cardinality $k$:

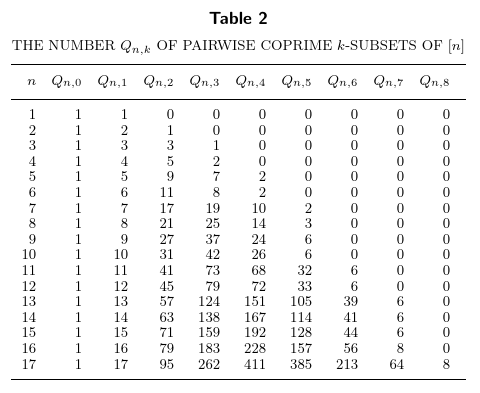
This time, the alternating sums equal $0$. Lastly, letting $R_{n,k}$ be the number of product-free subsets of $[n]$ of size $k$, we see that the alternating sums are $0$ in this case as well:

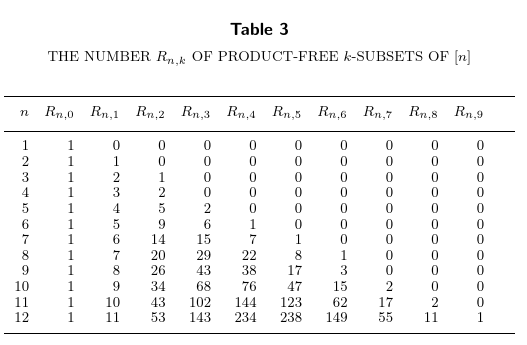
The sequences $P_{n,k}$, $Q_{n,k}$, and $R_{n,k}$ are in the OEIS as A355145, A355146, and A355147, respectively. Miscellaneous facts about these quantities were collected in the following proposition of our paper (this post follows the paper’s numbering).

Proposition 3. For $n\ge 2$ we have

1. $P_{n,1} = Q_{n,1} = n$ and $R_{n,1} = n-1$;
2. $P_{n,2} = \sum_{i=2} (i-d(i))$, where $d(i)$ counts the number of divisors of $i$;
3. $Q_{n,2} = \sum_{i=2}^n \varphi(i)$, where $\varphi$ is Euler’s totient function;
4. $R_{n,2} = {n\choose 2} - n -\lceil \sqrt n\rceil + 2$; and
5. for any $p$ prime and $k\ge 3$, $F(p,k) = F(p-1,k) + F(p-1, k-1)$, where $F$ can be any of $P$, $Q$, or $R$.

Partition-intersecting families

To unify the three examples above, we now introduce the class of set families mentioned in the top of the post. Let ${\cal F}$ be a family of finite sets of positive integers. Let $F_{n,k}$ be the number of elements of cardinality $k$ in \({\cal F}_n = {\cal F}\cap 2^{[n]}\). We would like to study the alternating sum $\sum_{k=0}^n (-1)^k F_{n,k}$. We will say that an element $S$ of \({\cal F}_n\) is maximal if for all $x\in [n]\setminus S$, \(S\cup \{x\}\notin {\cal F}_n\).

Now for the actual definition. We say that a set family \({\cal F}\) is \(m\)-partition-intersecting if for all $n\ge 2$, the following three conditions are satisfied (condition 2 does not depend on $n$ but conditions 1 and 3 do):

1. $[n]\notin {\cal F}_n$.
2. {\cal F} is downward closed; that is, for every $S\in {\cal F}$, every subset $T$ of $S$ is also in ${\cal F}$.
3. The set \(M_n\subseteq {\cal F}_n\) of maximal elements can be partitioned into $m$ disjoint nonempty classes $M_n = C_1 \sqcup \cdots\sqcup C_m$ such that for all $i$, the intersection $\bigcap_{S\in C_i} S$ is nonempty, and for all $i\ne j$ and any $S\in C_i$ and $T\in C_j$, $S\cap T = \emptyset$.

We are now able to state the main theorem.

Theorem 1. Let \({\cal F}\) be $m$-partition-intersecting and let $n\ge 2$. For $0\le k < n$, let \(F_{n,k}\) be the number of \(S\in {\cal F}_n = {\cal F}\cap 2^{[n]}\) with $|S|=k$. Then

\[\sum_{k=0}^{n-1} (-1)^k F_{n,k} = 1-m.\]

The proof of this theorem uses some basic results from enumerative combinatorics, relating the Möbius function of a poset to the homology of a certain simplicial complex.

From here, we just need to show that primitive sets, pairwise coprime sets, and product-free sets are all families that fit in our class:

Corollary 4. _For $n\ge 2$,

1. $\sum_{k=0}^n (-1)^k P_{n,k} = -1$;
2. $\sum_{k=0}^n (-1)^k Q_{n,k} = 0$; and
3. $\sum_{k=0}^n (-1)^k R_{n,k} = 0$.

A generalisation of primitive sets

A primitive set is a set that does not contain more than one multiple of any integer. We make this definition more general by forbidding sets with more than $s$ multiples of any given integer, and when $s=1$ we recover the definition of a primitive set. For $s\ge 2$, the family of $s$-multiple sets is not $m$-partition-intersecting for any $m$, but we still have the following theorem.

Theorem 5. Let $s\ge 2$ be an integer, let $n>s$, and let \(P_{s,n,k}\) denote the number of $s$-multiple subsets of $[n]$ with cardinality exactly $k$. We have

\[\sum_{k=0}^n (-1)^k P_{s,n,k} = (-1)^s {n-2\choose s-1}.\]

The proof of this also goes through the homology groups of a certain simplicial complex, but this time the calculations involved are more technical.