Rosie Zhao and I have just uploaded our paper “Arithmetic subsequences in a random ordering of an additive set” to the arXiv. In its simplest form, the problem we consider is the following. Given an ordering of the numbers $1$ through $n$, what is the length of the longest arithmetic subsequence that is embedded in this permutation? For example, in the ordering $(2,7,1,6,3,4,5)$, the longest arithmetic subsequence is $(2,3,4,5)$, which has length $4$. If we store the permutation in an array, the problem of finding the length of the longest arithmetic subsequence is a popular programming interview question that can be solved efficiently using dynamic programming (it is a medium-difficulty problem on LeetCode). But if we take the ordering to be random, with each of the $n!$ possibilities occurring with equal probability, then the length $L_n$ of the longest arithmetic subsequence becomes a random variable. Our paper studies the asymptotic behaviour of $L_n$ as $n$ gets large.
Update. (28 Sep 2021) Our paper was accepted to Integers: Electronic Journal of Combinatorial Number Theory! There were some small errors in the original lemmas, which have been corrected in both the published and arXiv versions as well as in the blog post below.
The integer case
Let $[1,n]$ denote the discrete interval ${1,2,\ldots,n}$. We regard an arithmetic progression in a sequence to be a subsequence
\[\big(a,a+r,a+2r,\ldots,a+(k-1)r\big),\]where $a$ is called the base point, $r$ is the step size, and $k$ is the length. Traditionally, arithmetic progressions are studied as subsets of some larger set, and one is interested in finding out if sets contain long arithmetic progressions as subsets. In our case, we start with the arithmetic progression $[1,n]$, scramble its elements into a sequence, and look for a long subsequence. For small $n$, using the dynamic programming techniques mentioned above, one can exhaustively compute the distribution of the longest arithmetic subsequence $L_n$. Letting $f_n(k)$ denote the number of permutations of $[1,n]$ whose longest arithmetic subsequence is of length $k$, we have the following table (click to enlarge):
Notice that each row sums to $n!$, since there are $n!$ orderings of $[1,n]$, and we can compute probabilities by simply dividing; for example, the probability that $L_9 = 3$ is $168368/(9!)\approx 46.4\%$. The first main result of our paper is the following theorem:
Theorem 4. Let $L_n$ denote the longest arithmetic sequence in an ordering of $[1,n]$, chosen uniformly at random. There exists a function $\psi(n)$ with $\psi(n)\sim 2\log n/\log\log n$ such that the probabilility that $L_n$ is not in the interval $[\psi(n)-6, \psi(n)+1]$ tends to $0$ as $n$ approaches infinity.
(In fact, we proved a slightly more general form of this theorem in the paper, considering $[1,n]^d\subseteq {\bf Z}^d$ for $d\geq 1$ and finding a function $\psi(n,d)\sim 2d\log n/\log\log n$.) To prove the theorem, we let $N_k$ denote the number of arithmetic subsequences of length $k$ in the random ordering. By the union bound, we have \({\bf P}\{L_n\geq k\}\leq {\bf E}\{N_k\}\), which goes to $0$ if $k\geq \psi(n)+1$. Then by the second moment method, it can be shown that
\[{\bf P}\{L_n < k\} = {\bf P}\{N_k= 1\} \le { {\bf V}\{N_k\}\over {\bf E}\{ {N_k} \}^2 } = {k^5\over P_n(k)/k!},\]where $P_n(k)$ is the number of arithmetic sequences of length $k$ that use elements of the set $[1,n]$. This approaches $0$ when $k<\psi(n)-6$. By a counting argument, one can show that
\[{\bf E}\{N_k\} \sim {n^2\over k!(k-1)},\]which can be inverted to show that $\psi(n)\sim 2\log n/\log\log n$.
Cyclic groups
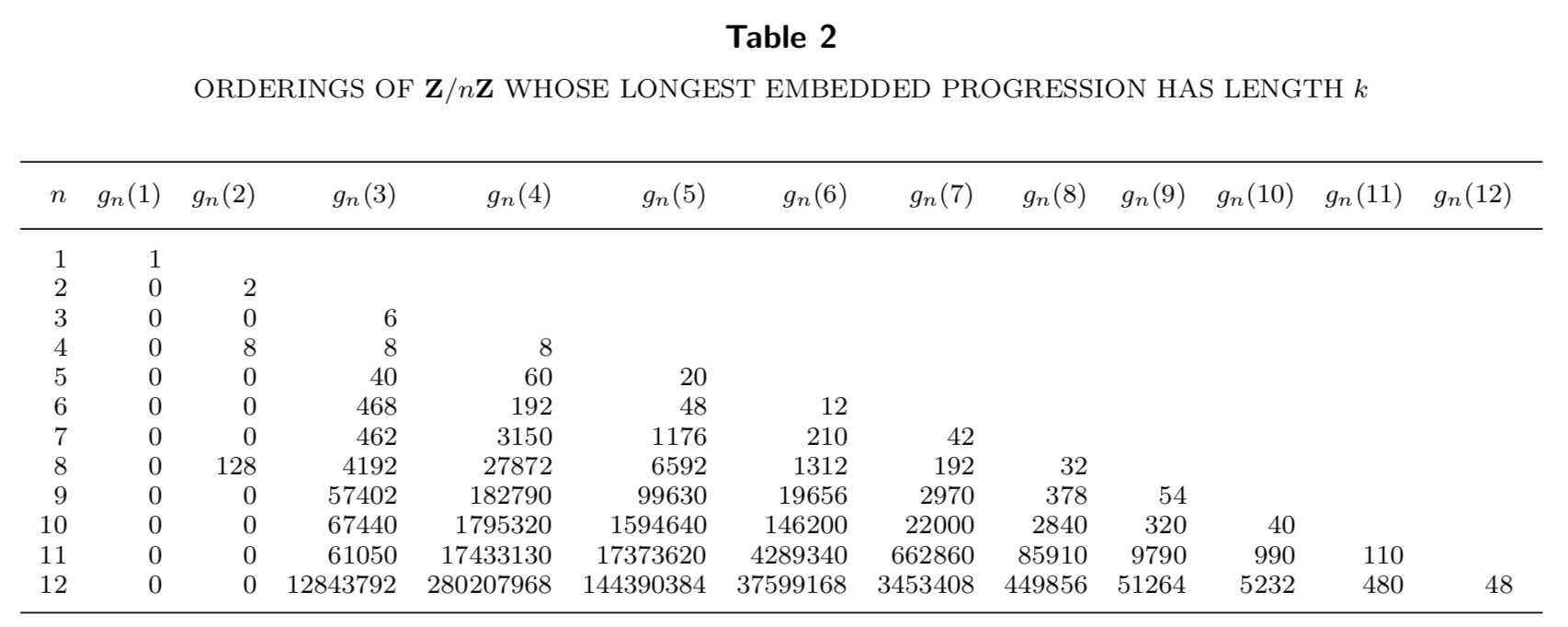
If we consider addition in the cyclic group ${\bf Z}/n{\bf Z}$, then $L_n$ is larger, since any arithmetic progression in $[1,n]\subseteq {\bf Z}$ is also a progression in ${\bf Z}/n{\bf Z}$, but not the other way around. For example, the sequence $(0,2,6,1,3,5,4)$ has the $4$-term arithmetic subsequence $(0,6,5,4)$ when addition is taken modulo $7$ (the base point is $0$ and the step size is $6$), but it has no arithmetic subsequence of length $4$ when the addition is ordinary integer addition. The distribution of $L_n$ for small $n$ in the cyclic case looks like this ($g_n(k)$ is the cyclic analogue of $f_n(k)$ from Table 1):
We prove the following analogue of Theorem 4 in the cyclic case:
Theorem 7. For a positive integer $n$, let $L_n$ denote the longest arithmetic subsequence in an ordering of ${\bf Z}/n{\bf Z}$, chosen uniformly at random. There exists a function $\chi(n)$ with $\chi(n)\sim 2\log n/\log\log n$ such that $L_n$ is in the interval $[\chi(n)-6, \chi(n)+1]$ with probability tending to $1$ as $n\to\infty$.
Note that while both $\psi(n)$ from Theorem 4 and $\chi(n)$ from Theorem 7 both have the same leading asymptotic term, we always have $\psi(n)<\chi(n)$. A closer look at Table 2 also reveals some interesting curiosities regarding $L_n$ in the cyclic case. Firstly, \({\bf E}\{L_n\}\) does not increase monotonically with $n$ as in the integer case. For example, we have \({\bf E}\{L_7\} = 4.25\) and \({\bf E}\{L_8\}\approx 4.136\). This is because there are “more ways” to form arithmetic subsequences in permutations of ${\bf Z}/n{\bf Z}$ when $n$ is prime. We also notice that there are only permutations without arithmetic subsequences of length $3$ when $n$ is a power of $2$. This can be formulated as the following theorem:
Theorem 8. The number $g_n(2)$ of orderings of ${\bf Z}/n{\bf Z}$ that do not contain any arithmetic subsequence of length $3$ equals $2^{n-1}$ if $n=2^m$ for some $m\geq 1$, and is zero otherwise. Any ordering of ${\bf Z}/2^m{\bf Z}$ that contains no progression of length $3$ consists of $2^{m-1}$ elements of the same parity, followed by the remaining $2^{m-1}$ elements of the opposite parity.
The proof was by induction in the case that $n$ is a power of $2$, and for $n$ not a power of $2$ we can reduce to the case where $n$ is an odd prime.
Possible noncommutative generalisations
The first and second moment methods we used did not rely on the fact that the groups we considered (${\bf Z}^d$ and ${\bf Z}/n{\bf Z}$) are abelian. One could extend these results to random orderings of other finite groups, such as the dihedral group $D_n$ or the symmetric group $S_n$. In the noncommutative case, one needs to specify whether the step size is multiplied by the base point on the left or on the right, but if the sequence contains every element of the (finite) group, then the distribution of $L_n$ will be the same for both choices.